ЭКОНОМИЧЕСКАЯ ШКОЛА

100 Hot Books (Амазон, Великобритания)

Дж. Харшаньи, Р. Зельтен  Общая теория выбора равновесия в играх / Пер. с англ. Ю.М. Донца, Н.А. Зенкевича, Л.А. Петросяна, А.Е. Лукьяновой, В.В. Должикова под редакцией Н.Е. Зенкевича — СПб. : Экономическая школа, 2001. — 424 с.

1.2. Кооперативные и бескоалиционные игры

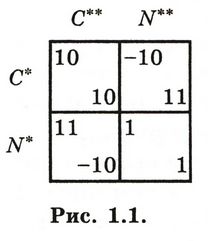
В классической теории игр кооперативные и бескоалицион­ные игры трактуются совершенно по-разному, и различие между этими двумя классами игр играет весьма важную роль. Нэш [33, 35], который первым ввел это различие, определил кооператив­ные игры как игры, допускающие как свободный обмен инфор­мацией, так и принудительные соглашения между игроками, в отличие от бескоалиционных игр, не допускающих ни свободно­го обмена информацией, ни принудительных соглашений.

Однако бинарное различие, основанное на одновременном вы­полнении двух критериев, логически неудовлетворительно. Мы не можем определить одну категорию как класс всех объектов, обладающих обоими свойствами А и В, а другую категорию как класс всех объектов, не обладающих ни одним из этих свойств. Если мы это сделаем, тогда необходимо спросить, как же быть с объектами, обладающими свойством А, но не свойством В, и с объектами, обладающими свойством В, но не А?

Поэтому предпочтительно использовать различие по одному критерию — определять кооперативные игры просто как игры, допускающие принудительные соглашения, а бескоалиционные игры — как игры, не допускающие таких соглашений. Во мно­гих случаях имеет значение и допустимый объем обмена инфор­мацией между игроками, но это оказывается менее важным во­просом. Для иллюстрации проблемы рассмотрим представлен­ную на рисунке 1.1 игру «дилемма заключенного». (Объяснение термина «дилемма заключенного» см. в [29, р. 94-95]).

В каждой клетке таблицы выигрышей число в верхнем ле­вом углу представляет выигрыш игрока 1, а чи­сло в нижнем правом углу — выигрыш игро­ка 2. Строки таблицы представляют стратегии С* и N* игрока 1, столбцы — стратегии С** и N** игрока 2.

Поскольку игра абсолютно симметрична между двумя игроками, оба игрока имеют равные по силе возможности. Поэтому естественно ожи­дать, что они согласятся с исходом, обеспечивающим обоим рав­ные выигрыши — посредством выбора либо пары стратегий С = (С*, С**), которая дала бы выигрыши (10, 10), либо пары стра­тегий N = (N*, N**), которая дала бы выигрыши (1, 1). Если игра проводится как кооперативная (допускающая принудительные соглашения), то игроки, действуя рационально, несомненно сра­зу согласятся применить пару стратегий С, так как С даст им значительно более высокие выигрыши, чем N. Таким образом, С = (С* С**) можно назвать кооперативным решением игры.

Напротив, если игра проводится как бескоалиционная (т. е. если игроки не могут заключать принудительные соглашения), то им в лучшем случае остается использовать пару стратегий N = (N*, N**), которую можно назвать некооперативным реше­нием.

Чтобы обосновать это положение, мы вначале покажем, что если принудительные соглашения невыполнимы, то рациональ­ные игроки не могут выбрать пару стратегий С = (С* С**). Даже если бы они и согласились использовать свои С-стратегии, они не могли бы рационально ожидать, что каждый другой игрок бу­дет придерживаться этого соглашения; что совершенно лишает смысла любое подобное соглашение. Предположим, что им необ­ходимо заключить такое соглашение и каждый ожидает, что дру­гой будет его придерживаться. В таком случае игрок 1 тотчас получил бы стимул к нарушению этого соглашения, применяя стратегию N*, а не С*, так как его наилучшим ответом¹ на ожи­даемую стратегию С** игрока 2 была бы N*, а не С*.

В бескоалиционной игре рациональные игроки не могут вы­брать пару стратегий С, так как она была бы самодестабилизи­рующейся: расчет одного из игроков на то, что другой будет при­держиваться С-стратегии, дает явный стимул отклониться от С. Наш анализ также показывает и математическую причину, по которой С имеет это нежелательное свойство. Она состоит в том, что С-стратегии обоих игроков не составляют наилучшие ответы друг на друга. Напротив, наилучшим ответом на С** является N*, а наилучшим ответом на С* будет N**.

Для сравнения: рациональные игроки могут без труда реа­лизовать в бескоалиционной игре пару стратегий N = (N* N**), так как она является самостабилизирующейся: поскольку N* и N** взаимно составляют два наилучших ответа друг на друга, и если оба игрока по какой-либо причине ожидают друг от друга применения N-стратегии, то они будут иметь явный стимул ре­ализовать это ожидание, применяя N-стратегии.

Решающий вопрос в этой игре состоит в наличии у игроков возможности заключать принудительные соглашения, и практи­чески не имеет значения, разрешено ли им разговаривать друг с другом. Наличие возможности договариваться и обсуждать усло­вия соглашения не окажет реальной помощи, если шансов на выполнение этого соглашения мало. Обсуждение условий согла­шений полезно только тогда, когда правила игры делают их обя­зывающими и принудительными. (В реальной жизни принуди­тельное исполнение соглашений внешне обеспечивается судами, правительственными организациями или давлением обществен­ного мнения; внутренне их исполнение может быть обеспечено нежеланием нарушать соглашения по моральным причинам и их осведомленностью о том, что именно так обстоит дело).

Как уже отмечал Нэш [33, 35], аналогичные соображения применимы ко всем бескоалиционным играм. Поскольку в та­ких играх соглашения не имеют принудительного характера, ра­циональные игроки всегда будут выбирать набор стратегий, ко­торый является

самостабилизирующимся в том смысле, что игроки будут иметь некоторый стимул придерживаться набора стратегий (или, по крайней мере, не будут иметь стимула не делать этого), если они ожидают, что все другие игроки будут поступать так же. Математически это означает, что они всегда будут выбирать набор стратегий с таким свойством, чтобы стра­тегия каждого игрока была наилучшим ответом на все страте­гии других игроков. Набор стратегий с этим свойством называ­ется равновесием (ситуацией равновесия). Кроме того, Нэш по­казал, что каждая конечная игра² имеет по крайней мере одну ситуацию равновесия (в чистых стратегиях или иногда только в смешанных стратегиях).

Тем не менее определения кооперативных и бескоалицион­ных игр все еще нуждаются в дальнейшем разъяснении. В су­ществующем виде они могут произвести ложное впечатление, будто бескоалиционные игры невозможно использовать для мо­делирования игровых ситуаций, в которых игроки могут за­ключать принудительные соглашения (или связывать себя обя­зательствами перед другой фирмой,³ например неотменяемыми обещаниями и угрозами). Как мы увидим в разделе 1.3, самообя­зывающие ходы можно явно включать в развернутую форму бес­коалиционной игры.

Поэтому мы предлагаем переформулировать наши определе­ния следующим образом. Бескоалиционная игра — это игра, мо­делируемая в предположении, что игроки неспособны заключать принудительные соглашения (или связывать себя иными обя­зательствами), за исключением тех случаев, когда развернутая форма игры в явном виде наделяет их способностью это де­лать. Напротив, кооперативная игра — это игра, моделируемая в предположении, что игроки способны

заключать принудитель­ные соглашения (и, возможно, связывать себя иными обязатель­ствами), даже если их способность это делать не показана в яв­ном виде развернутой формой игры.

Координация материалов. Экономическая школа

Контакты