1.3. Неотменяемые обязательства_Харшаньи

100 Hot Books (Амазон, Великобритания)

Дж. Харшаньи, Р. Зельтен Общая теория выбора равновесия в играх / Пер. с англ. Ю.М. Донца, Н.А. Зенкевича, Л.А. Петросяна, А.Е. Лукьяновой, В.В. Должикова под редакцией Н.Е. Зенкевича — СПб. : Экономическая школа, 2001. — 424 с.

1.3. Неотменяемые обязательства в бескоалиционной игре

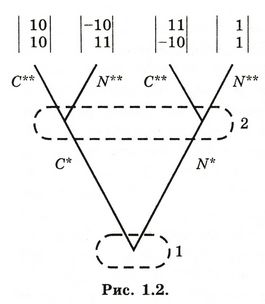
Существует несколько способов включения самообязывающих ходов в развернутую форму игры. Например, выигрыши можно определить так, чтобы любое нарушение игроком обязательства повлекло серьезные наказания, или можно включить в игру дополнительных игроков, задача которых состояла бы в наказании нарушителей. Но простейший способ состоит в следующем. В подходящей точке дерева игры мы предоставляем соответствующему игроку право выбора между двумя ходами, скажем α и β, где α интерпретируется как обязательство что-либо сделать или не сделать на некотором дальнейшем этапе (этапах) игры, а β — как несвязывание себя обязательством. Обязательство, представленное ходом α, может быть безусловным или может стать действенным условно в зависимости от наступления некоторых будущих событий. Если игрок выбирает ход β, то начиная с этого момента игра будет определяться остальной частью дерева исходной игры, которую мы будем называть поддеревом Т. Но если он выбирает ход α, то начиная с этого момента игра будет определяться модифицированным вариантом поддерева Т, который обозначим через Т'. Т' будет отличаться от Т тем, что на нем будут удалены все ветви, соответствующие ходам, нарушающим обязательство, взятое на себя данным игроком при выборе хода а (т. е. ходы, нарушающие обязательство, будут просто недоступны этому игроку).

Конечно, может случиться и так, что устранение ходов, нарушающих обязательство, оставит некоторые из информационных множеств игроков с одной-единственной ветвью (одним-единственным ходом); это означает, что у него более нет реальной альтернативы ни в одном из этих информационных множеств. Такие информационные множества (и эти единственные ветви) всегда можно опустить, так как информационные множества, не допускающие реальной альтернативы, не имеют значения. Этот метод можно легко обобщить на случаи, когда игрок может выбирать не только между связыванием и несвязыванием себя конкретным обязательством, но и из ряда альтернативных обязательств, Например, развернутая форма игры, обсуждавшейся в разделе 1.2, может быть представлена деревом игры на рисунке 1.2. Числа 1 и 2, расположенные справа от двух символов (двух овалов) информационных множеств, указывают, какой игрок имеет ход в данном информационном множестве.

Теперь способность игроков заключить принудительное соглашение по применению своих С-стратегий мы можем представить следующим образом. В начале игры мы предоставляем игроку 1 возможность сделать выбор из ходов α* и β*, где α* означает «я обязуюсь применять стратегию С* при условии, что игрок 2 обязуется применять стратегию С**», тогда как β* означает «я не беру на себя никаких обязательств». Если игрок действительно выбрал ход α*, мы предоставляем теперь игроку 2 возможность выбора из ходов α** и β**, где α** означает «да, я действительно обязуюсь применять стратегию С**, как предложил игрок 1», а ход β** означает «я не беру на себя никаких обязательств».

Теперь можно выделить три класса.

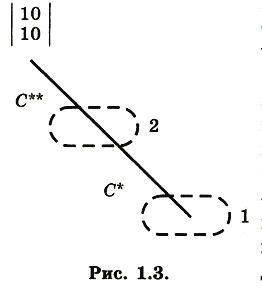
1. Если игрок 1 выберет α*, а игрок 2 выберет α**, то оба игрока будут обязаны применять свои С-стратегии. Следовательно, остальная
часть игры теперь сведется к поддереву Т₁, показанному на рисунке 1.3.

Но, так как каждое из этих двух информационных множеств на Т₁ имеет лишь одну исходящую из него ветвь, мы можем опустить оба информационных множества и обе ветви (С* и С**), что сводится к замене всего поддерева Т₁ на вектор выигрышей , порожденный этим поддеревом.

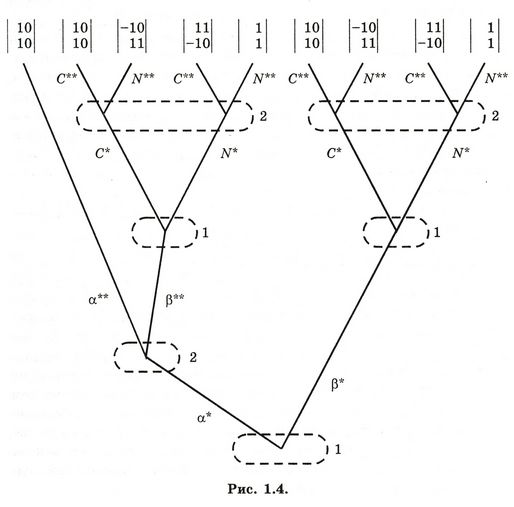
2. Если игрок 1 выберет α*, а игрок 2 выберет β*, то оба игрока не будут связаны обязательством по ограничению своей свободы действий. Следовательно, остальная часть игры будет определяться поддеревом T₂, которое является лишь копией дерева исходной игры.

3. Если игрок 1 выберет (β*, то игроки еще раз сохранят свою свободу действий, а остальная часть игры будет определяться поддеревом Т₃, которое опять-таки будет лишь копией дерева исходной игры.

Дерево расширенной игры, соответственно, показано на рисунке 1.4.

В нормальной форме расширенной игры мы можем охарактеризовать стратегии каждого игрока тремя символами. Например, первый символ

(α* или β* для игрока 1 и α** или β** для игрока 2) может использоваться для обозначения выбора игроком между связыванием и несвязыванием себя обязательством, второй символ (С* или N* для игрока 1 и С** или N**для игрока 2) может обозначать стратегию, которой он будет придерживаться на поддереве Т₂, а третий символ (С* или N* или, альтернативно, С** или N**) может обозначать стратегию, которой он будет придерживаться на поддереве Т₃. Таким образом, одной из возможных стратегией игрока 1 будет α*C*N*. Очевидно, что каждый из игроков будет иметь 2³ = 8 различных чистых стратегий.

Нетрудно проверить, что расширенная игра имеет одну совершенную ситуацию равновесия в чистых стратегиях: Е₁ = (α*N*N*, α**N**N**). Иными словами, если оба игрока способны связать себя обязательствами по применению С-стратегий, то очевидно, что в их интересах делать это, чтобы получить выигрыши (10, 10). В то же время определение E₁ содержит два символа N* и два N**. Они указывают на то, что каждый игрок будет применять свою N-стратегию, если противник откажется взять на себя обязательство по применению своей С-стратегии. (Конечно, эта часть стратегического плана каждого из игроков не будет реализована, так как противник возьмет на себя требуемое обязательство).

Интуитивно Е₁ можно отождествить с кооперативным решением

(С*, С**) исходной игры. Поэтому можно утверждать, что, включая обязательные ходы α* и α** (а также необязательные ходы β* и β**) в развернутую форму игры, мы, по существу, превращаем кооперативное решение (С*, С**) в ситуацию равновесия, чтобы трансформировать ее в исход, достигаемый рациональными игроками, даже если игра (или, точнее, расширенная версия игры) проводится как формально бескоалиционная. Действительно, поскольку Е₁ — единственная ситуация совершенного равновесия расширенной игры, мы превратили Е₁ в единственный исход, согласующийся с рациональным поведением обоих игроков. (Более подробный анализ расширенной игры см. в разделе 1.14. Как мы постараемся показать в разделах 1.9 и 1.10, с рациональным поведением игроков в бескоалиционной игре совместимы только ситуации совершенного равновесия).

вернуться

Координация материалов. Экономическая школа

ЭКОНОМИЧЕСКАЯ ШКОЛА

Контакты