ЭКОНОМИЧЕСКАЯ ШКОЛА

100 Hot Books (Амазон, Великобритания)

Дж. Харшаньи, Р. Зельтен  Общая теория выбора равновесия в играх / Пер. с англ. Ю.М. Донца, Н.А. Зенкевича, Л.А. Петросяна, А.Е. Лукьяновой, В.В. Должикова под редакцией Н.Е. Зенкевича — СПб. : Экономическая школа, 2001. — 424 с.

1.8. Проблема неустойчивости: новое обоснование применения ситуаций равновесия в смешанных стратегиях

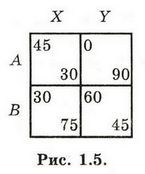
     Чтобы проиллюстрировать проблему неустойчивости, постав­ленную играми, имеющими лишь равновесия в смешанных стра­тегиях, рассмотрим игру, представленную на рисунке 1.5.

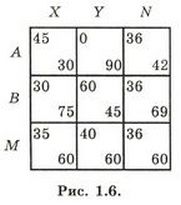
Единственное равновесие в этой игре существует в сме­шанных стратегиях и имеет вид  Е = (М, N), где М = (1/3, 2/3) и N = (4/5, 1/5) (т. е. равновесная стра­тегия М игрока 1 приписывает вероятности 1/3 и 2/3 его двум чистым стратегиям А и В соответ­ственно, а равновесная стратегия N игрока 2 при­писывает вероятности 4/5 и 1/5 его двум чистым стратегиям X и У). Чтобы облегчить анализ этой игры, мы добавим в матрицу выигрышей новую строку, соответ­ствующую М, и новый столбец, соответствующий N (рис. 1.6).

Как можно видеть из расширенной матрицы выигрышей, если игрок 1 ожидает, что игрок 2 применит свою равновесную стра­тегию N, то игрок 1 не будет иметь реального стимула приме­нить свою равновесную стратегию М. Это объясняется тем, что он получит одинаковый выигрыш и₁ = 36 независимо от того, применит он смешанную равновесную стратегию М, либо одну из своих двух чистых стратегий А и В, либо любую смешанную стратегию, отличную от М. Точно так же игрок 2 не будет иметь реального стимула применить свою равновесную стратегию N, даже если он ожидает, что игрок 1 приме­нит равновесную стратегию М. Причина заключается в том, что игрок 2 получит одинаковый выигрыш и₂ = 60 независимо от того, применит он свою равновесную стратегию N, одну из своих чистых стратегий X и Y, либо любую смешанную стратегию, отличную от N.

     Именно это мы имеем в виду, когда говорим, что ситуация равновесия Е = (М, N) (по-видимому) неустойчива: даже если она не порождает стимул для каждого из игроков не применять свою равновесную стратегию, она не порождает и стимул, который сде­лал бы привлекательным для него применение собственной рав­новесной стратегии.

Теперь будем утверждать, что неустойчивость таких ситуа­ций равновесия в смешанных стратегиях лишь кажущаяся. Даже если игроки обладают максимально возможной и полной инфор­мацией о матрице выигрышей в игре, у каждого игрока всегда будет оставаться некоторый неуменыпаемый минимум неопре­деленности относительно действительных выигрышей другого игрока. Например, даже если матрица выигрышей показывает, что связанный с парой стратегий (А, X) выигрыш игрока 2 ра­вен Н₂ (А, X) = 30, игрок 1 никогда не сможет исключить воз­можность того, что именно в данный момент этот выигрыш в действительности может составить 30 - ε или 30 + ε, где ε — малое положительное число. Это объясняется тем, что функция полезности для каждого лица зависит по меньшей мере от неко­торых весьма малых непредсказуемых случайных изменений в силу перемен в его настроении или, быть может, из-за внезапно­го побуждения применить одну из своих чистых стратегий, бо­лее предпочтительную, чем другая.

     Это означает, что реалистическая модель любой данной игры будет иметь не фиксированные, а случайно изменяющиеся вы­игрыши, при том изменения могут быть весьма малы. Математи­ческий анализ показывает, что такая игра не будет иметь ситуа­ций равновесия в смешанных стратегиях.⁴ Вернее, все ее ситуа­ции равновесия будут в чистых стратегиях в том смысле, что ни один игрок не будет преднамеренно рандомизировать выбор между двумя своими чистыми стратегиями. Вместо этого он всегда уста­новит, что одна из его двух чистых стратегий даст ему более высокий ожидаемый выигрыш, и именно эту стратегию он в дей­ствительности будет применять.

      В то же время можно показать, что случайные изменения выигрышей двух игроков будут взаимодействовать таким обра­зом, что игрок 1 будет считать стратегию А более выгодной, чем стратегия В, в течение почти 1/3 времени, а стратегию В более выгодной, чем стратегия А, в течение почти 2/3 времени. В ре­зультате, хотя игрок 1 может и не предпринять попытку рандо­мизировать, он будет применять свои две чистые стратегии почти точно с вероятностями, предписанными его равновесной страте­гией М = (1/3,2/3), Кроме того, хотя игрок 2 может и не предпри­нять попытку рандомизировать, он будет применять свои две чистые стратегии X и У почти точно с вероятностями, предпи­санными его равновесной стратегией N = (4/5,1/5), (Более подроб­ное обсуждение и математические доказательства см. [12].)

      В заключение отметим, что, когда данная игра интерпрети­руется как игра с фиксированными выигрышами, она не дает

⁴ Наша теория предполагает, что случайные колебания в выигры­шах определяются абсолютно непрерывным совместным распределе­нием вероятностей.

игрокам стимулов к применению в ситуации равновесия в сме­шанных стратегиях своих чистых стратегий с вероятностями, предписанными их равновесными стратегиями. Однако если игра, что более реалистично, интерпретируется как игра со случайно изменяющимися выигрышами, то она дает требуемые стимулы, и поэтому исчезает проблема неустойчивости, связанная с ситуаци­ями равновесия в смешанных стратегиях.

вернуться

Контакты