ЭКОНОМИЧЕСКАЯ ШКОЛА

100 Hot Books (Амазон, Великобритания)

Дж. Харшаньи, Р. Зельтен Общая теория выбора равновесия в играх / Пер. с англ. Ю.М. Донца, Н.А. Зенкевича, Л.А. Петросяна, А.Е. Лукьяновой, В.В. Должикова под редакцией Н.Е. Зенкевича — СПб. : Экономическая школа, 2001. — 424 с.

1.9. Проблема несовершенства

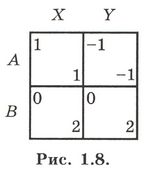
Чтобы проиллюстрировать проблему несовершенства, рассмот­рим игру в развернутой форме, так как в нормальной форме за­частую неясно различие между ситуациями совершенного и не­совершенного равновесия. В качестве примера рассмотрим игру в развернутой форме, показанную на рисунке 1.7.

Первый ход в этой игре делает игрок 1. Он может выбрать один из ходов, А или В. Если он выберет В, игра сразу закончится с выигрышами u₁ = 0 и и₂ = 2. Если он выберет А, игрок 2 также получит возможность

выбрать один из двух ходов, X или У. Если он выберет X, выигрыши будут и₁ = и₂ = 1; если же он выберет У, выиг­рыши будут u₁ = и₂ = -1. Нормальная форма этой игры показана на рисунке 1.8.

Таким образом, у игрока 1 есть две чистые стратегии: стратегия А («выб­рать ход А») и стратегия В («выбрать ход Б»). У игрока 2 также есть две чи­стые стратегии: стратегия X («выбрать ход X, если игрок 1 выбрал А») и стра­тегия У («выбрать ход У, если игрок 1 выбрал А»).

Очевидно, игра имеет две ситуации равновесия в чистых стратегиях: пары стратегий Е₁ = (А, X) и Е₂ = (В, У). Е₁ является ситуацией совершенного равновесия, а Е₂ — ситу­ацией несовершенного равновесия, включающей иррациональные стратегии.

Стратегия У требует, чтобы игрок 2 выбрал ход У, который, несомненно, иррационален, так как дает ему и игроку 1 выигрыш u₁ = и₂ = -1, даже несмотря на то, что выбором хода X они оба получили бы выиг­рыш u₁ = и₂ =1. В равной мере иррациональна и стратегия В: игрок 1 должен знать, что если он выберет ход А, то игрок 2, несомненно, выберет ход X, который даст ему выигрыш и₁ = 1; поэтому игрок 1 не должен выбирать ход B, который дает ему лишь u₁ = 0.5.⁵

Почему оказывается возможным положение, когда ситуация равновесия должна включать такие иррациональные стратегии? В частности, почему ситуация равновесия может потребовать, что­бы игрок выбрал ход, подобный У, когда выбор этого хода проти­воречит максимизации его собственного выигрыша?

Ответ заключается в том, что ход, подобный У, уменьшает ожидаемый выигрыш игрока только тогда, когда этот ход реализу­ется с положительной вероятностью. Однако если эти два игро­ка действуют в соответствии с ситуацией равновесия Е₂ = (В, У), то игрок 2 никогда не переместится в позицию, где необходимо реализовать этот иррациональный ход У. Иными словами, ход У реализуется с нулевой вероятностью и поэтому не уменьшает ожидаемый выигрыш игрока 2.

По определению, равновесная стратегия должна максимизи­ровать ожидаемый выигрыш соответствующего игрока, если стра­тегии других игроков остаются неизменными. Это означает, что ни одна из равновесных стратегий не может предписывать ирра­циональный (не максимизирующий выигрыш) ход в любом ин­формационном множестве, который достигается с положитель­ной вероятностью, если все игроки применяют свои равновесные стратегии. Но равновесная стратегия может предписывать ирра­циональный ход игроку в любом информационном множестве, достигаемом с нулевой вероятностью. Ситуации несовершенного равновесия — это именно те ситуации равновесия, которые пред­писывают ход, противоречащий максимизации выигрыша в некотором

⁵ Е₂ = (В, У) является «нежелательной» ситуацией равновесия, при­чем не только потому, что она несовершенна, но еще и потому, что ис­пользует нестрого доминируемую стратегию (поскольку стратегия У нестрого доминируется стратегией X). Можно показать, что в любой игре, содержащей лишь два информационных множества, ситуация не­совершенного равновесия всегда будет включать по крайней мере одну нестрого доминируемую стратегию. Но эта теорема не верна для игр, содержащих три или более информационных множества. Поэтому про­блема, поставленная несовершенными равновесиями, не может быть све­дена к проблеме, определяемой доминируемыми равновесиями.

информационном множестве, достигаемом с нулевой вероятностью.

Эти соображения приводят к следующему выводу. Если игра содержит достаточное число случайных ходов, то каждое инфор­мационное множество будет достигаться с некоторой положитель­ной вероятностью независимо от применяемых игроками страте­гий. Игра, обладающая этим свойством, будет содержать только ситуации совершенного равновесия. Это обстоятельство может быть использовано для формального математического определе­ния ситуаций совершенного и несовершенного равновесия [43]. Более того, как мы увидим в главе 2, оно также может быть использовано и для исключения из игры всех ситуаций несовер­шенного равновесия. Чтобы убедиться в том, что решение, полу­чаемое для каждой игры G, будет ситуацией совершенного равно­весия, применим нашу теорию не к этой игре G, а к равномерно возмущенной игре в стандартной форме с полной памятью G', полученной из G.⁶

Интуитивно игра G' будет получена в предположении, что каждый раз, когда игрок i захочет применить данную чистую стратегию ф_i он будет допускать различные «ошибки» с малыми, но положительными вероятностями. В частности, если стратегия ф_i. требует, чтобы он сделал ход ф_ij в своем j-м информационном множестве, мы будем иметь малую вероятность ε > 0 осуществления другого хода (ф’_{ij ≠} ф_ij) вместо этого. Для простоты сделаем допущение о равномерности, чтобы эта вероятность ошибки ε

⁶ Для каждой игры с полной памятью ее нормальная форма с агента­ми будет иметь в точности те же ситуации равновесия, что и исходная игра в развернутой форме (или, что равнозначно, в своей нормальной форме; см. [43]). Но в общем случае это не верно для игр с неполной памятью. В силу данного обстоятельства мы будем всегда предпола­гать, что любая рассматриваемая нами игра смоделирована как игра с полной памятью. Предположение не является ограничивающим, так как каждая игра с неполной памятью может быть легко преобразована в игру с полной памятью. Это объясняется тем, что любая игра с непол­ной памятью всегда основывается на рассмотрении некоторой команды (команд) — некоторого множества (множеств) игроков с идентичными интересами — как одного игрока (игроков) и поэтому всегда может быть преобразована в игру с полной памятью посредством рассмотре­ния каждого члена любой такой команды как отдельного игрока. На­пример, бридж иногда моделируется как игра двух лиц с неполной па­мятью. Но ее можно столь же легко моделировать как игру четырех лиц с полной памятью.

была одинаковой для всех игроков i во всех информационных множествах и для всех пар альтернативных ходов ф_ij и ф'_ij, до­ступных в любом данном информационном множестве. В силу допущения о равномерности полученная игра G' будет называть­ся равномерно возмущенной игрой.⁷

⁷ Мы будем придерживаться принципа, согласно которому в отсут­ствие доводов в пользу противного наш анализ данной игры всегда бу­дет основываться на предположении о равномерности, а следовательно, и на игре с равномерными возмущениями. Предположение о равномер­ности составляет весьма полезную часть нашей теории: оно представ­ляется вполне естественным, и к тому же во многих случаях оно суще­ственно упрощает вычисление решения. Несмотря на это, оно не явля­ется совершенно необходимым предположением нашей теории.

Если кто-либо считает, что у него есть достаточные причины пола­гать, что в данной игре G ошибки игроков будут соответствовать нерав­номерному распределению вероятностей, то ему остается лишь выбрать конкретное семейство неравномерных распределений вероятностей оши­бок П_ε, которое он сочтет уместным, и использовать эти распределения П_ε для построения соответствующих неравномерно возмущенных нор­мальных форм с агентами G_ε игры G. В таком случае он может приме­нить нашу теорию решения к этим играм с возмущениями G_ε.

С другой стороны, если бы анализ любой игры G основывался на таком семействе распределений вероятностей ошибок П_ε, то последнее пришлось бы включить в определение этой игры G наряду с другими определяющими характеристиками, такими как множества стратегий игроков и функции выигрыша.

Таким образом, если бы две игры имели одинаковые нормальные формы с агентами, но в силу предположения имели бы различные рас­пределения вероятностей ошибок П_ε, то их пришлось бы рассматривать как две различные игры с, возможно, различными решениями

вернуться

Координация материалов. Экономическая школа

Контакты