ЭКОНОМИЧЕСКАЯ ШКОЛА

Дж. Харшаньи, Р. Зельтен  Общая теория выбора равновесия в играх / Пер. с англ. Ю.М. Донца, Н.А. Зенкевича, Л.А. Петросяна, А.Е. Лукьяновой, В.В. Должикова под редакцией Н.Е. Зенкевича — СПб. : Экономическая школа, 2001. — 424 с.

1.10. Ситуации несовершенного равновесия, сослагательные условные предложения и самообязывающие ходы

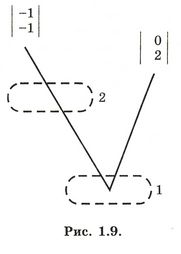
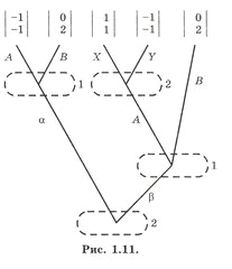
В современной логике проблема, поставленная ситуациями несовершенного равновесия, может быть переформулирована сле­дующим образом. Предположение, что игрок 2 применит страте­гию Y, эквивалентно условному высказыванию S, «если бы иг­рок 1 сделал ход А, то игрок 2 сделал бы ход У». Если это услов­ное высказывание интерпретировать в материальном смысле, оно автоматически становится вырожденно истинным каждый раз, когда не возникает сформулированное условие (осуществление

⁷ Мы будем придерживаться принципа, согласно которому в отсут­ствие доводов в пользу противного наш анализ данной игры всегда бу­дет основываться на предположении о равномерности, а следовательно, и на игре с равномерными возмущениями. Предположение о равномер­ности составляет весьма полезную часть нашей теории: оно представ­ляется вполне естественным, и к тому же во многих случаях оно суще­ственно упрощает вычисление решения. Несмотря на это, оно не явля­ется совершенно необходимым предположением нашей теории.

Если кто-либо считает, что у него есть достаточные причины полагать, что в данной игре G ошибки игроков будут соответствовать нерав­номерному распределению вероятностей, то ему остается лишь выбрать конкретное семейство неравномерных распределений вероятностей оши­бок П_ε, которое он сочтет уместным, и использовать эти распределения для построения соответствующих неравномерно возмущенных нор­мальных форм с агентами G_ε игры G. В таком случае он может приме­нить нашу теорию решения к этим играм с возмущениями G_ε.

С другой стороны, если бы анализ любой игры G основывался на таком семействе распределений вероятностей ошибок П_ε, то последнее пришлось бы включить в определение этой игры G наряду с другими определяющими характеристиками, такими как множества стратегий игроков и функции выигрыша.

Таким образом, если бы две игры имели одинаковые нормальные формы с агентами, но в силу предположения имели бы различные рас­пределения вероятностей ошибок П_ε, то их пришлось бы рассматривать как две различные игры с, возможно, различными решениями.

хода А игроком 1). Но если это высказывание S интерпретиру­ется как сослагательное условное (каковым оно, конечно, явля­ется грамматически), оно будет просто ложным. Если игрок 1 все же делает ход А, тогда игрок 2 (в предположении, что он рацио­нальный индивид, старающийся максимизировать свой выигрыш) скорее всего не сделает ход У.

Пара стратегий Е₂ = (В, У) формально образует ситуацию рав­новесия. Для того чтобы это было так, необходимо лишь, чтобы высказывание S было истинным, когда оно интерпретируется в материальном смысле. (В математике принято рассматривать любое условное высказывание как истинное, если оно истинно при интерпретации в материальном смысле.) Тем не менее наша теоретико-игровая интуиция расценивает Е₂ как ситуацию ирра­ционального равновесия, так как эта интуиция признала бы ис­тину высказывания S только при условии, что стал истинным в случае его интерпретации как сослагательного условного, что оче­видно не так.

Наше различие между ситуациями совершенного и несо­вершенного равновесия тесно связано с вопросом, могут ли игро­ки брать на себя твердое обязательство в бескоалиционной игре (см. разделы 1.2 и 1.3). Игра, которую мы обсуждали, не содер­жит самообязывающих ходов. Поэтому наш анализ основывался на предположении, что игрок 2 не может заранее связать себя обязательством выбрать ход X вместо У в тот момент, когда он достигнет информационного множества, в котором должен быть сделан этот выбор. Однако легко видеть, что при возможности взять на себя такое обязательство игрок 2 был бы явно заинтере­сован поступить именно так (чтобы испугать игрока 1 и заста­вить его сделать ход А вместо В). Правильный способ позволить игроку 2 взять на себя такое обязательство состоит в предостав­лении ему возможности сделать самообязывающий ход в начале игры вместо того, чтобы неправильно истолковать игру, не содер­жащую самообязывающего хода, словно она имеет такой ход.

Добавить желательный самообязывающий ход можно следу­ющим образом. В начале игры мы разрешаем игроку 2 сделать выбор из ходов α и β, где α может быть интерпретирована как высказывание «я обязуюсь выбрать ход У, если игрок 1 выберет ход А», a β может быть интерпретирована как высказывание «я не беру на себя никаких обязательств». Если игрок 2 выбе­рет β, будущие ходы в игре будут определяться поддеревом T_β, являющимся точной копией дерева ис­ходной игры. Напротив, если он выберет α, ходы в игре будут определяться под­деревом Т_α, которое отличается от дере­ва исходной игры отсутствием хода X (он был устранен самообязывающим ходом α игрока 2).

Как только будет опущена ветвь X, мы сможем убрать все информационное множество, из которого исходила ветвь X (так как в этой точке у игрока 2 больше не останется реального выбора), вместе с множеством, состоящим из остававшей­ся единственной ветви У, но не другие эле­менты Т_а. Этот приведенный вариант поддерева Т_а будет называться поддеревом Т_α*. На рисун­ках 1.9 и 1.10 показаны поддеревья T_α и Т_α*, а на рисунке 1.11 — дерево новой расширенной игры.

В нормальной форме новой игры каждый иг­рок будет иметь четыре различные чистые стра­тегии. Стратегиями игрока 1 будут АА, АВ, ВА и ВВ, где первая буква всегда обозначает ход, кото­рый сделал бы игрок 1 в поддереве Т_α*, а вторая буква обозначает ход, который сделал бы он в поддереве T_β. Чистыми стратегиями игрока 2 являются αХ, αY, βХ и βY.

Легко проверить, что новая игра имеет только одну ситуа­цию совершенного равновесия в чистых стратегиях, а именно Е₁^* = (ВА, аХ). Е₁^* интерпре­тируется следующим образом. В начале игры игрок 2 обязу­ется сделать ход Y, если игрок 1 сделает ход А. Это удержит иг­рока 1 от совершения хода А Вместо этого он сделает ход В, который даст выигрыши (0, 2), как того желает игрок 2. (Если бы игрок 2 не взял на себя обязательство сделать ход А, игроки использовали бы взамен пару стратегий (B, У)). Интуитивно мы можем отождествить E₁^* с парой стратегий Е₂ = (В, Y) исходной игры лишь с тем отличием, что в исходной игре эта пара страте­гий была ситуацией несовершенного равновесия, тогда как в но­вой расширенной игре E₁^* является ситуацией совершенного рав­новесия, и при том единственной ситуацией совершенного рав­новесия новой игры.

Это, разумеется, вовсе не удивительно. Как только игрок 2 сможет связать себя обязательством по применению стратегии Y, связывание этим обязательством становится для него весьма ра­циональным, и тогда применение стратегии В также становится рациональным для игрока 1, как того желает игрок 2 (более по­дробный анализ расширенной игры см. в разделе 1.15).

вернуться

Координация материалов. Экономическая школа

Контакты