Уильям Баумоль Фирма и ее цели

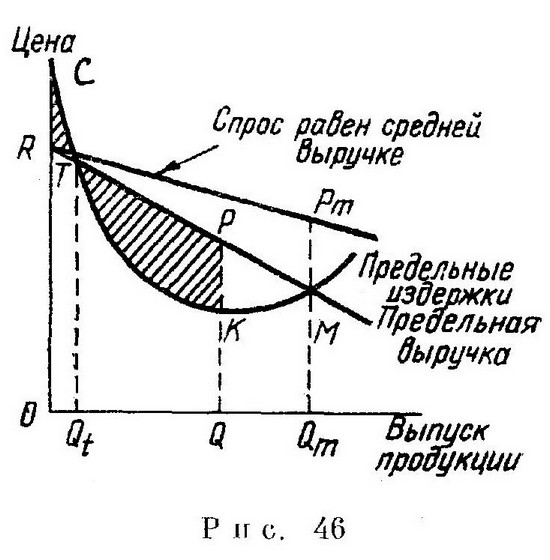
ФИРМА И ЕЕ ЦЕЛИ (Уильям Баумоль, гл.10 учебника «Экономическая теория и исследование операций.М.Прогресс,1965»)

Принятие фирмой тех или иных решений предполагает, как мы уже видели, наличие данных о спросе на выпускаемые ею товары и издержках их производства. Но нахождение оптимального решения требует также знания целей, которые ставит перед собой предприниматель. Решение, наилучшим образом отвечающее одним целям, не всегда соответствует достижению других целей.

1. Альтернативные цели фирмы

Для определения целей фирмы (или ее руководства) не существует простого метода. Несомненно лишь одно. Весьма часто последним, у кого следует спрашивать о целях, которые преследует определенный индивидуум, является сам этот индивидуум (это совершенно ясно показали психологи). Разговаривая с предпринимателями, обычно приходишь к выводу, что они добиваются любой разумной цели, о какой бы вы их ни спросили. Они утверждают, что хотят максимизировать объем продаж, а также максимизировать прибыль, что они стремятся к придачу минимизировать издержки и т. д. К сожалению, однако, одновременно добиться достижения такого множества целей обычно невозможно.

Предположим, например, что ассигнования на рекламу в размере 0,5 млн. долл. минимизируют удельные затраты, ассигнования в размере 1,2 млн. долл. максимизируют совокупную сумму прибыли, в то время как при ассигнованиях в 1,8 млн. долл. максимизируется объем продаж фирмы. Одновременно реализовать все три решения невозможно, поэтому фирма должна остановиться на одном из них или каком-либо компромиссном решении.

Не одни предприниматели, естественно, страдают от желания одновременно решить несколько несовместимых задач. Насколько легко поддаться искушению добиваться одновременно нескольких заманчивых целей, настолько же трудно отказаться хотя бы от одной из них. Это испытали даже самые опытные люди. Именно поэтому один великий экономист вынужден был заметить, что в известном тезисе о «максимальном благе для максимального числа людей» одно «максимальное» лишнее.

В экономическом анализе наиболее распространенной является предпосылка о стремлении любой фирмы максимизировать общую сумму прибыли. Однако нет оснований считать, что все предприниматели преследуют одинаковую цель. Например, владелец небольшой фирмы, в которой он занят лично, может стремиться к максимизации своего свободного времени при условии, что его доходы превышают некоторый минимальный уровень. Имеют место случаи, когда по совету врача перегруженные работой предприниматели отказывались от суливших прибыль хозяйственных операций.

В результате некоторых наблюдений высказывалась также мысль, что фирмы зачастую стремятся максимизировать общую сумму продаж (валовой доход) при условии, что прибыль не падает ниже некоторого минимального, граничащего с допустимым уровня. Иначе говоря, пока прибыль находится на удовлетворительном уровне, основные силы и средства фирмы направлены на увеличение объема продаж. Это, в частности, может быть объяснено либо стремлением предприниматели сохранить конкурентоспособность своей фирмы, которая во многом зависит и от размеров предприятия, либо интересами управляющих (в отличие от интересов акционеров), поскольку их жалованье в большей мере зависит от объема продаж, нежели от суммы прибыли, либо попросту соображениями престижа.

Во всяком случае, не дело исследователя операций или экономиста учить предпринимателя, каковы должны быть его цели, хотя они в состоянии помочь сформулировать эти цели, а иногда и показать предпринимателю реальность постановки более смелых задач. Цели фирмы надо принимать такими, какими они заданы, а задача исследователя — сделать вытекающие из них выводы, то есть описать, что делают предприниматели для достижения этих целей и, возможно, предложить более эффективные пути их достижения.

В экономическом анализе и при изучении хозяйственных проблем методами исследования операций основная трудность заключается в том, что характер целей фирмы заранее не известен. Прежде чем перейти к построению моделей и основанным на них вычислениям, важно определить характер целей фирмы. Как и следует ожидать, многие выводы из анализа с изменением целевой функции также претерпят изменения. Но, как мы покажем ниже, изменение целей может, иногда довольно неожиданно, оставить неизменными некоторые существенные зависимости. Весьма удобно заранее выявить эту особенность, если она имеет место, еще до анализа той или иной конкретной проблемы. Ибо если существуют проблемы, оптимальные решения которых аналогичны, независимо от того, какая выбрана фирмой целевая функция, то можно избежать предшествующей анализу сложной работы по определению целей фирмы.

2. Фирма, максимизирующая прибыль

Прежде всего рассмотрим традиционную теорию фирмы, максимизирующей прибыль. В главе о дифференциальном исчислении основное предельное условие максимизации прибыли выводится в качестве иллюстрации. Указанное условие — «предельные издержки равны предельной выручке» — мы получим еще раз графически и с помощью логических рассуждений.

Предпосылка заключается в том, что фирма получает максимум прибыли лишь при условии, что ее предельные издержки и предельная выручка равны (по меньшей мере приблизительно), то есть при условии, что добавочная единица выпуска продукции приносит выручку, равную издержкам производства этой единицы, так что предельная прибыль равна нулю¹.

Это легко доказать. Предположим, фирма производит 200 тыс. единиц какого-либо изделия х и при данном уровне производства предельная выручка от продажи единицы х равна 1,1 долл. при предельных издержках, равных лишь 96 центам. Каждая добавочная единица принесет поэтому чистый доход 14 центов, так что, сохраняя выпуск на уровне 200 тыс. единиц, фирма не максимизирует прибыль. Равным образом при предельных издержках, превышающих предельную выручку, фирма также не максимизирует прибыль, так как она пренебрегает возможностью экономии — снижение выпуска уменьшило бы выручку, но в еще большей мере позволило бы снизить издержки.

Условие равенства предельных издержек и предельной выручки можно вывести также с помощью графика (см. рис. 46). При любом выпуске OQ валовая выручка представлена поверхностью OQPR под кривой предельной выручки (см. правило 9 главы 3). Равным образом совокупные издержки представлены поверхностью OQKC непосредственно под кривой предельных издержек. Общая прибыль как разница между валовой выручкой и совокупными издержками представлена, следовательно, разницей между двумя поверхностями — слегка заштрихованной ТКР, отображающей

-----------------------------------------------------

¹ Слово «приблизительно» добавлено потому, что на практике точного совпадения иногда достичь невозможно. 230 773-й

автомобиль может дать прибыль 2 долл., а 230 774-й автомобиль может дать убыток, так что предельные издержки совпадут с предельной выручкой при выпуске, например, 230 773_3/4-го автомобиля, что нереально.

общую сумму прибыли, и густо заштрихованной RTC. Очевидно, что при движении из точки Q вправо площадь поверхности прибыли ТКР возрастает. Лишь при объеме выпуска OQ_m эта площадь достигает максимума (поверхность ТКМР). Но при выпуске OQ_m предельные издержки равны предельной выручке, поскольку действительно пересечение кривых предельных издержек и предельной выручки не дает возможности при дальнейшем движении вправо (дальнейшем увеличении выпуска) расширить площадь, представляющую общую сумму прибыли. Следовательно, мы еще раз установили, что в точке максимальной прибыли предельные издержки и предельная выручка должны быть равны.

Прежде чем закончить рассмотрение данного вопроса, целесообразно подчеркнуть, что обратная теорема неверна. Уровень производства, при котором предельные издержки и предельная выручка равны, не обязательно максимизирует прибыль.

Равенство предельных издержек и предельной выручки имеет место при нескольких уровнях производства, но некоторые из них далеки от максимальной прибыли. На рис. 46 указанное равенство соблюдается при выпусках OQ_t и OQ_m. Однако при OQ_t фирма терпит чистые убытки (отрицательная прибыль), представленные густо заштрихованной поверхностью RTC. Движение из точки Q_t влево означает, что издержки снижаются в большей мере, чем выручка; при движении вправо выручка

возрастет в большей мере, чем издержки. Следовательно, выпуск OQ_t соответствует минимальной прибыли, хотя здесь и соблюдено условие максимизации прибыли (равенство пре дельной выручки и предельных издержек).

Мы сумеем объяснить этот неожиданный результат, вспомнив, что условие «предельная прибыль равна нулю» означает лишь то, что в этом положении ни незначительное увеличение объема продукции, ни его уменьшение не изменяют величины прибыли. Другими словами, мы достигли такого выпуска, при котором кривая общей суммы прибыли (на графике она не показана) не поднимается и не опускается. Однако этим свойством обладают не только точки максимума (выпуск, обеспечивающий максимальную прибыль), но и точки минимума (выпуски, приносящие минимальную прибыль). Иначе говоря, имеются точки нулевой предельной прибыли, в которых предельные издержки равны предельной выручке¹.

Мы приходим к выводу, что, хотя при выпуске, максимизирующем прибыль, предельные издержки равны предельной выручке, обратное утверждение неверно; следовательно, выпуск, удовлетворяющий условию равенства предельных издержек и предельной выручки, не обязательно максимизирует прибыль.

3. Применение: установление цен и изменение издержек

Предыдущая теорема позволяет сделать некоторые прогнозы относительно политики фирмы, стремящейся максимизировать прибыль, и сформулировать ряд обязательных правил ее поведения, выведенных методами исследования операций. Мы в состоянии определить не только оптимальный объем выпуска продукции, но, используя кривую спроса на продукт фирмы, также и цену, максимизирующую прибыль. Ибо, если известен оптимальный выпуск, мы можем установить по кривой спроса, какая цена позволит фирме продать соответствующее количество продукта, а это и есть оптимальная цена. На рис. 46 видно, что при оптимальном выпуске продукции OQ_m соответствующая цена есть Q_mP_m, где точка Р_т — точка на кривой спроса над Q_m (обратите внимание, что Р_т не является точкой пересечения кривых предельных издержек и предельной выручки).

В последнем параграфе главы 4 показано, как данная теорема позволяет предсказать характер влияния изменений налоговых ставок или других элементов издержек на выпуск продукции и цену. Нам достаточно выяснить, как эти изменения смещают кривую предельных издержек, чтобы, найдя новую точку пересечения кривых предельных издержек и предельной выручки, определить также новую комбинацию цены и объема продукции, максимизирующую прибыль. Вспомним один из выводов, необходимый для дальнейшего анализа, — теорему о влиянии изменения постоянных (фиксированных) издержек. Эти изменения никогда не оказывают какого-либо влияния на кривую предельных издержек фирмы (см. параграф 6 главы 3), ибо предельные постоянные издержки всегда равны нулю

-------------------------------------------------------

¹ Эта проблема возникает потому, что условие предельного максимума следует дополнить условием второго порядка: вторая

производная прибыли должна быть отрицательной; в настоящем контексте это означает, что кривая предельной выручки пересекает кривую предельных издержек сверху (слева направо). Читателю следовало бы убедиться, что это условие выполняется при выпуске OQ_m, максимизирующем прибыль (см. рис. 46), но не выполняется при OQ_f. Полезно было бы дать этому условию экономическую интерпретацию. См. параграф 5 главы 4.

(по определению, добавочная единица продукции ничего не добавляет к постоянным издержкам). Отсюда, если у фирмы, максимизирующей прибыль, возрастают арендная плата, налоги с имущества или другие постоянные издержки, то комбинация выпуск — цена, удовлетворяющая условию равенства предельных издержек и предельной выручки, остается неизменной. Другими словами, фирма, максимизирующая прибыль, не будет реагировать каким-либо изменением объема продукции или цены на любое изменение постоянных издержек. Этот довольно неожиданный вывод находится в явном противоречии с хозяйственной практикой и нуждается в дополнительных пояснениях, которые приводятся ниже.

4. Добавление. Множественность продуктов и затраты

Принятие фирмой решений об объеме и структуре продукции — процесс более сложный даже в принципе, чем это можно предположить из сказанного выше. Почти все фирмы производят ряд продуктов, и каждый из них требует денежных затрат и производственных мощностей. В любой данный момент времени возможности выпуска ограничены, и очень часто, когда фирмой принимается решение увеличить выпуск продукта х, это делается за счет продукта у. Иначе говоря, такая фирма не может просто увеличить производство продукта х до оптимального уровня, пренебрегая при этом тем влиянием, какое это решение окажет на выпуск продукта у.

Для фирмы, максимизирующей прибыль и принимающей во внимание оба продукта, мы имеем предельное правило как частный случай правила 2 (из главы 3).

Ограниченные ресурсы любого вида (включая капитальные вложения) должны быть распределены между двумя видами продукции х и у таким образом, чтобы предельная прибыль от затрат i при производстве х была равна предельной прибыли при производстве у.

Смысл данного правила самоочевиден. Если условие не соблюдается, фирма не может максимизировать прибыль, ибо, чтобы увеличить доходы, ей достаточно переключить часть затрат i с производства менее прибыльного продукта на производство более прибыльного.

Другими словами, последняя теорема гласит, что если фирма максимизирует прибыль, то при снижении выпуска продукта х, допустим, на 5 долл. высвобождаются производственные мощности С, позволяющие увеличить производство у ровно на 5 долл. Ибо это означает, что предельная эффективность высвобожденных мощностей одинакова при производстве продуктов х и у, а это как раз то. о чем говорит предыдущий вариант данного правила¹.

Заслуживает внимания еще одна формулировка этого же правила. Предположим, задана цена каждого продукта, не зависящая от

объема его производства. Тогда требуется, чтобы предельные издержки производства каждого продукта были пропорциональны

его цене, то есть МС_х/Р_х = МС_у/Р_у, где Р_х и МС_Х суть соответственно цена и предельные издержки производства продукта х и т.д.²

Выше рассматривались лишь те решения фирмы, стремящейся к максимизации прибыли, которые касаются выпуска продукции. Фирма должна принимать, конечно, и другие решения. В частности, она обязана определить величину затрат, включая издержки обращения (реклама, содержание торговых агентов и т. д.). Для этих решений также имеются аналогичные правила, изложенные в предыдущей главе и в параграфе 6 главы 14. Основным из них является то, что максимизация прибыли для любого фактора затрат i и у предполагает

MP_i/MP_i= МP_j/MP_j,

где через МР_iобозначена предельная прибыль от фактора i, через Р_i — его цена и т. д.

Теперь, когда мы выяснили последствия максимизации прибыли, посмотрим, какие особенности приносит принятие упоминавшегося альтернативного решения максимизировать валовую выручку при условии, что прибыль фирмы не падает ниже некоторого заданного минимального уровня.

------------------------------------------------------

¹ Предыдущее правило говорит о том, что предельная прибыль должна быть одинакова в обоих случаях, тогда как теперь мы имеем

равенство предельной выручки при производстве изделий x и у. Но, поскольку единица фактора стоит D долл., предельная прибыль

от i при производстве х (МР_ix) равна предельной выручке минус издержки, так что при условии равенства в обоих случаях

предельной прибыли мы получаем

MP_ix = MR_ix- D = MR_iy- D - MP_iy ,

следовательно, MR_ix = MR_iy и наоборот.

² Чтобы увидеть, как это вытекает из предыдущего варианта правила, предположим, что один доллар затрат позволяет выпустить на

К долл. продукта х и па К долл. продукта у. Значит, если единица продукта х требует 5 долл. затрат (предельные издержки равны 5

долл.), то единица х стоит (примерно) 5 К долл. Равным образом, если выпуск единицы у обходится в 9 долл., то эта единица должна

стоить 9 К долл. Отсюда мы получаем

МС_x/Р_x = 5/5K = 9/9K = MC_y/Р_у.

5. Нахождение комбинации цена — выпуск.

Максимизация объема продаж

Максимизация объема продаж при ограничении, налагаемом величиной прибыли, не равноценна стремлению добиться максимального объема продукции в натуральном измерении (который нелегко поддается определению в условиях выпуска продукции широкого ассортимента, что характерно для современной фирмы). Скорее она означает максимизацию валового дохода (суммы продаж в долларах), служащего для предпринимателя наглядным мерилом объема реализованной продукции. В этом смысле максимальный объем продаж не обязательно предполагает очень высокий физический объем продукции. Если взять крайний случай — нулевую цену, то денежная выручка равна нулю при каком угодно высоком объеме продукции.

Обычно условию максимизации объема продаж в долларах удовлетворяет определенный уровень производства. Этот р уровень находится с помощью известного правила о том, что максимизация выручки достигается только при таком объеме выпуска, при котором эластичность спроса равна 1, то есть когда предельная выручка равна нулю. Это условие заменяет правило «предельные издержки равны предельной выручке», которое действует при максимизации прибыли.

Однако это правило пренебрегает ограничением, налагаемым прибылью. А именно, если при объеме производства, максимизирующем выручку, фирма получает прибыль достаточную или более чем достаточную, чтобы выдержать конкуренцию, то она будет стремиться именно к такому уровню производства. Если же при этом объеме продукции прибыль слишком мала, то выпуск должен быть изменен с тем, чтобы он удовлетворял условию получения некоторого минимума прибыли, даже в ущерб максимизации объема продаж.

Мы видим, следовательно, что представляются возможными два типа равновесия: при одном из них условие получения прибыли не служит эффективным препятствием на пути максимизации выручки, при другом — оно является таким препятствием. Это иллюстрируется соответствующим графиком (см. рис. 47), на котором построены кривые валовой выручки, издержек и прибыли фирмы.

Уровни производства, при которых максимизируются прибыль и объемы продаж, представлены соответственно через ОQ_p и OQ_s. Если, например, заданная минимальная прибыль есть ОР₁, то выпуск OQ_s, максимизирующий продажи, гарантирует также получение достаточной прибыли, а потому он удовлетворит фирму. В этом случае продажная цена равна Q_sR_s/OQ_s . Если же минимальная прибыль задана как ОР₂, то объем производства OQ_s, приносящий прибыль Q_sP_s, явно не подходит. Вместо этого выпуск снижается до уровня OQ_c, как раз удовлетворяющего новому условию в отношении прибыли.

Ниже доказывается, что фактически только те точки равновесия, где ограничительное условие эффективно (то есть OQ_c, а не OQ_s), встречаются обычно, когда принимаются в расчет прочие решения фирмы.

Выпуск OQ_p, максимизирующий прибыль, обычно меньше тех выпусков, которые максимизируют объем продаж, будь то OQ_s или OQ_c. Это доказывается с помощью известного правила о том, что в точке максимальной прибыли предельные издержки равны предельной выручке. Действительно, предельные издержки, как правило, числа положительные (мы не можем обычно выпускать дополнительную продукцию без дополнительных издержек). Отсюда при максимуме прибыли предельная выручка также представлена положительным числом, то есть дальнейшее увеличение выпуска продукции приведет к увеличению объема продаж (валовой выручки). Следовательно, если в своей максимальной точке прибыль превышает заданный минимум¹, то в целях

максимизации общего объема продаж окажется выгодным снизить цену и увеличить физический объем продукции.

6. Реклама

Решение фирмы о размере расходов на рекламу также может в значительной мере определяться выбором цели — стремится ли фирма к максимизации объема продаж или прибыли. Графически это представляется довольно просто. На рис. 48 на горизонтальной оси откладываются расходы на рекламу, на вертикальной — общий объем продаж (валовая выручка) и суммарная прибыль. Форма кривой валовой выручки позволяет сделать вывод, к которому, по-видимому, склоняется большинство предпринимателей, что увеличение расходов на рекламу всегда приносит увеличение физического объема продаж,

---------------------------------------------------------

¹ Если при таком объеме выпуска фирма получает меньше заданного минимума, то выпуска, удовлетворяющего условию в

отношении прибыли, видимо, не существует.

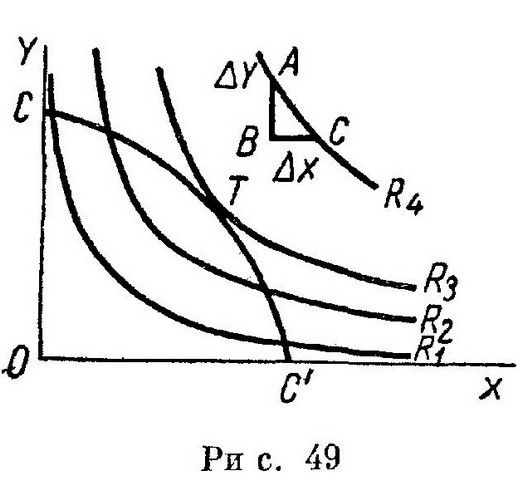
хотя в некоторой точке выручка может начать резко убывать¹. Это означает, что валовая выручка должна меняться точно таким же

образом, как расходы на рекламу, ибо в отличие от снижения цен, увеличение ceteris paribus расходов на рекламу не влечет за собой изменения рыночной ценности продаваемых товаров. Отсюда увеличение физического объема продаж в связи с дополнительными ассигнованиями на рекламу должно всегда сопровождаться пропорциональным увеличением валовой выручки, тогда как увеличение физического объема продаж, обусловленное снижением цен, может либо привести, либо не привести к росту валовой выручки, в зависимости от того, эластичен или неэластичен спрос по отношению к ценам.

Если добавить к расходам на рекламу все прочие издержки, то мы получим линию, отображающую совокупные издержки (производства и обращения) как функцию расходов на рекламу. Вычитая эти совокупные издержки из валовой выручки, мы получим кривую совокупной прибыли РР'.

Из графика видно, что максимизация прибыли достигается в точке М кривой РР' при расходах ОА_р. Если, с другой стороны, допустимый минимум прибыли фирмы, максимизирующей выручку, представлен ОР₁, то уровень расходов на рекламу, обеспечивающий максимальный объем продаж и удовлетворяющий условию в отношении прибыли, есть ОА_с. Следует отметить, что возможность существования не ограниченного максимального объема продаж, аналогично выпуску OQ_s на рис. 47, исключена. Ибо, по предположению, увеличение расходов па рекламу всегда влечет за собой, в отличие от снижения цен, увеличение валовой выручки. Как следствие, предпринимателю, максимизирующему объем продаж, всегда выгодно увеличивать расходы на рекламу до тех пор, пока прибыль не уменьшится до минимально допустимого уровня. Это означает, что фирма, максимизирующая выручку, будет ассигновать на рекламу не меньше, а обычно больше, чем фирма, максимизирующая прибыль. ------------------------------------------------------------

¹ Это, конечно, не всегда верно, поскольку чрезмерная реклама способна, очевидно, и оттолкнуть потенциальных покупателей.

Следует, кстати, заметить, что при более глубоком анализе необходимо учитывать взаимозависимость решений о расходах на рекламу и ценах. Это можно осуществить с помощью графика в трехмерном пространстве, где оси представляют цену, расходы на рекламу и выручку (и издержки).

Ибо существует возможность, соблюдая условие в отношении прибыли, увеличить расходы на рекламу несколько больше уровня ОА_р, максимизирующего прибыль, если только уровень А_рМ не больше заданного минимума ОР₁. Более того, такое увеличение расходов на рекламу желательно, так как, по предположению, оно приведет к увеличению физического объема продаж и вместе с ним и к пропорциональному росту выручки.

Взаимозависимость решений об объеме выпуска продукции и о расходах на рекламу позволяет теперь обосновать высказанное ранее суждение о том, что неограниченного, максимизирующего объем продаж выпуска OQ_s (см. рис. 47), обычно не существует. В самом деле, если цена установлена на уровне, обеспечивающем достижение подобного уровня производства, то прибыль превысит минимальный уровень и окажется выгодным увеличить продажу путем увеличения расходов на рекламу, услуги и т. п. Это непосредственно вытекает из теоремы о том, что не испытывающего ограничений уровня рекламы, максимизирующего прибыль, обычно не существует. Поскольку предельная эффективность рекламы всегда суть величина положительная, реклама может быть всегда использована для увеличения продаж до такого объема, когда прибыль будет доведена до минимального уровня.

7. Выбор комбинаций затраты — выпуск

Типичная фирма выпускает широкий ассортимент изделий (зачастую число названий выражается сотнями или даже тысячами) и использует, естественно, множество факторов производства. В настоящем параграфе кратко рассматривается влияние максимизации объема продаж (а не прибыли) на объем и распределение различных видов затрат и выпуска.

Полученный результат на первый взгляд выглядит довольно неожиданно: при заданном уровне расходов фирма, максимизирующая сумму продаж, будет производить точно такое же количество каждого вида продукции и продавать ее точно так же, как и фирма, максимизирующая прибыль. Равным образом при заданном объеме валовой выручки фирмы обоих типов оптимально будут использовать те же факторы и в равных количествах и распределять их идентичным образом. Этот вывод может показаться неправдоподобным, так как принято считать, что одни товары и рынки сбыта приносят большую прибыль и меньшую выручку, нежели другие, поэтому логично предположить, что фирма, максимизирующая прибыль, сосредоточит ресурсы на выпуске одних товаров, а фирма, максимизирующая выручку, — на других. Но мы сейчас увидим, почему это не так.

Наш вывод легко проиллюстрировать графически. Пусть на рис. 49 х и у обозначают реализованные количества двух различных товаров (или продажи одного товара на двух различных рынках) или купленные количества двух факторов. Кривые R₁, R₂ и т. д. суть кривые равной выручки, то есть любая такая кривая есть геометрическое место всех комбинаций х и у, приносящих некоторую фиксированную сумму выручки. Равным образом кривая СС' представляет все комбинации х и y, которые могут быть произведены при некоторой заданной сумме издержек. Из традиционного анализа известно, что течка касания Т кривой СС' и одной из кривых семейства R представляет максимальную прибыль. Но это есть также точка максимальной выручки, ибо она лежит на самой высокой кривой выручки, достижимой при заданных затратах. Это подтверждает наш вывод.

Немного поразмыслив, мы окончательно убедимся в обоснованности вывода. Дело в том, что поскольку при заданном уровне издержек прибыль есть разница между выручкой и издержками, все, что максимизирует прибыль, максимизирует и выручку. Значит, различия в структуре выпуска и в распределении факторов производства у фирм, максимизирующих прибыль и выручку, следует приписать большему объему производства (и, следовательно, суммарных издержек и выручки), сопровождающему, как мы видели, максимизацию выручки, а не перераспределению данного объема издержек (или выручки)¹.

В изложенном виде указанный вывод абсолютно тривиален. Стоит, однако, принять во внимание при максимизации выручки ограничение в отношении прибыли, как мы приходим к более интересному, но тесно связанному с предыдущим выводу.

Разницу между максимально достижимой прибылью и минимальным ее уровнем, которым довольствуется фирма, максимизирующая сумму продажи, мы вправе рассматривать в качестве фонда прибыли, приносимой в жертву в пользу возможно

---------------------------------------------------------------

¹ Мы приходим к выводу, что исследователь операций, стоящий перед проблемой распределения некоторого фиксированного

количества ресурсов, при заданных прочих переменных, входящих в решение, даст одинаковый ответ, независимо от того, максимизирует ли фирма объем продажи или прибыль. Вследствие указанной особенности достигается значительная экономия усилий исследователя. При распределении ресурсов, например, исследователь операций освобождается от утомительных попыток выяснения сравнительной важности выручки и прибыли в качестве целей фирмы.

большего увеличения выручки. Поскольку уровень выпуска каждого вида продукции превосходит точку максимальной прибыли, его предельная эффективность с точки зрения прибыли отрицательна. Другими словами, каждый раз, когда фирма увеличивает выпуск какого-либо продукта с целью увеличения валовой выручки, она должна прибегнуть к фонду приносимой в жертву прибыли. Указанный фонд должен быть распределен между отдельными продуктами и факторами, а также между рынками сбыта таким образом, чтобы максимизировалась общая сумма продаж. Здравый смысл подсказывает необходимость того, чтобы предельная эффективность — с точки зрения прироста выручки — доллара прибыли, принесенного в жертву, допустим, в пользу продукта х, была равна эффективности доллара, пожертвованного в пользу любого другого продукта у, то есть мы должны иметь

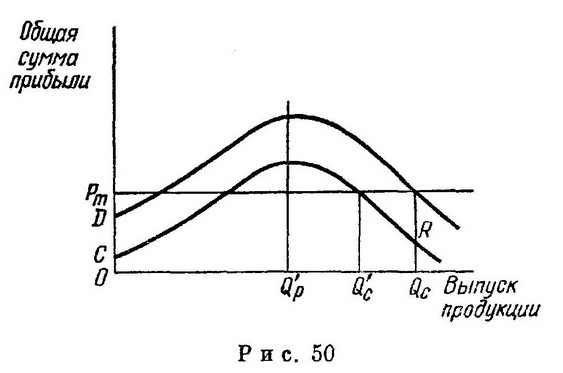
Данное соотношение указывает, что даже фирмы, стремящиеся к максимизации суммы продаж, должны избегать относительно малоприбыльных видов затрат и продукции, независимо от уровня общих издержек и общей выручки.

8. Установление цен и изменение накладных издержек и налогов

Изучающие предмет неизменно считают одним из наиболее поразительных выводов теории фирмы утверждение о том, что накладные издержки не оказывают влияния на решения о ценах и выпуске продукции¹. Этот вывод явно противоречит

хозяйственной практике, так как на деле увеличение издержек обычно заставляет серьезно подумать об увеличении цены. Нетрудно, однако, показать, что именно такой должна быть реакция фирмы, максимизирующей сумму продаж и рассматривающей прибыль не как высшую цель, а в качестве ограничения. Если в условиях равновесия фирма всегда получает прибыль, лишь удовлетворяющую ограничению, то рост накладных расходов должен означать падение прибыли ниже допустимого уровня. Это влечет за собой снижение выпуска продукции и (или) расходов на рекламу для восполнения необходимой суммы прибыли. Цель любого такого снижения производства заключается, естественно, в том, чтобы подготовить повышение продажной цены.

--------------------------------------------------------------

¹ См. параграф 9 главы 4. В параграфе 3 главы 7 показано, однако, что постоянные издержки влияют на решение о том, сколько и

каких производственных мощностей фирмы следует использовать в данном процессе производства.

Это легко показать на графике (см. рис. 50). Увеличение накладных расходов графически представлено равномерным сдвигом вниз кривой общей прибыли на расстояние, соответствующее этому увеличению. Значит, при росте накладных расходов на сумму CD выпуск с ОQ_c сокращается до ОQ'_c, ибо при OQ_c прибыль составит Q_cR, что ниже минимально допустимого уровня ОР_т. И наоборот, изменение накладных расходов оставляет неизменным максимизирующий прибыль уровень выпуска OQ'_p. Ибо увеличение издержек приводит к равномерному уменьшению высоты «холма прибыли», но, однако, не меняет абсциссы его вершины. Данный вывод затрагивает также налоговую политику. Иногда утверждают, что фирма бессильна предпринять что-либо для того, чтобы переложить часть выплачиваемого ими налога на покупателей или свой персонал. Фирма, максимизирующая прибыль, ничего не выиграет от

повышения цен или изменения выпуска продукции в качестве реакции на изменение налоговых ставок, если действует шкала, при которой чем выше прибыль фирмы до вычета налогов, тем больше остается после их уплаты. Доказательство этому почти такое же, как и в анализе накладных издержек. Налог с дохода корпораций снижает высоту кривой общей суммы прибыли, не сдвигая ее вершины ни вправо, ни влево.

Однако, если фирма желает максимизировать сумму продаж при условии обеспечения некоторого минимума, а не максимума прибыли, этот вывод опять-таки утрачивает силу. Рост налогов побудит фирму увеличить цену (а значит, уменьшить выпуск) с целью возмещения потерянной прибыли. Объяснить возможность переложения этого на первый взгляд неперело-жимого налога просто: фирма, максимизирующая сумму продаж, имеет, по сути дела, неиспользованный резерв прибыли (так как она ее не максимизировала), из которого она принуждена черпать при увеличении налогов, хотя это только вернет ей ее прежние прибыли за счет некоторого сокращения выручки.

Этим мы заканчиваем исследование последствий политики максимизации суммы продаж. В настоящем виде анализ имеет значение преимущественно для иллюстрации характера влияния выбора целей на оптимальные решения фирмы. Задача анализа заключалась в том, чтобы указать на могущие возникнуть серьезные ошибки в том случае, если исследованию поведения фирмы и ее политики не предшествует выяснение целей фирмы. Вернемся теперь к традиционному (связанному с максимизацией прибыли) анализу теории фирмы.

Вернуться

Координация материалов. Экономическая школа

ЭКОНОМИЧЕСКАЯ ШКОЛА

Контакты