ЭКОНОМИЧЕСКАЯ ШКОЛА

КОРРЕЛЯЦИЯ (correlation) — статистическое понятие, характеризующее степень связи между двумя переменными. Если две переменные обнаруживают тенденцию к совместному изменению, то говорят, что они коррелируют между собой, а степень, с которой они коррелируют, измеряется коэффициентом корреляции.

КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ (correlation coefficient) — статистический показатель (обычно обозначаемый буквой r), с помощью которого измеряется степень связи между двумя переменными. Если две переменные совершенно не связаны друг с другом, то коэффициент корреляции равен нулю; а если две переменные полностью связаны друг с другом, то абсолютная величина коэффициента корреляции равна единице. Высокий коэффициент корреляции между двумя переменными показывает только то, что они изменяются совместно, и отнюдь не предполагает причинно-следственную зависимость между ними, когда изменение одной переменной вызывает изменение другой.

Если высокие значения одной переменной соответствуют высоким значениям другой переменной, то говорят, что они положительно коррелируют. Если же высокие значения одной переменной соответствуют низким значениям другой переменной, то говорят, что они отрицательно коррелируют. Таким образом, коэффициенты корреляции могут варьировать в пределах от +1 (при абсолютной положительной связи) до -1 (при абсолютной отрицательной связи); при этом нулевое значение коэффициента корреляции указывает на отсутствие связи между двумя переменными.

Коэффициент корреляции служит также для измерения степени согласия линии регрессии (см. регрессионный анализ), которая рассчитывается для совокупности выборочных наблюдений методом наименьших квадратов. Если линия регрессии повышается слева направо и тесно согласуется с наблюдениями, то имеет место высокий положительный коэффициент корреляции; если же линия регрессии понижается слева направо и тесно согласуется с наблюдениями, то имеет место высокий отрицательный коэффициент корреляции. Если же уравнение регрессии содержит две или более независимые переменные, то для измерения точности, с которой плоскость, описываемая уравнением множественной регрессии, согласуется с наблюдаемыми значениями, можно использовать коэффициент множественной корреляции.

РЕГРЕССИОННЫЙ АНАЛИЗ (regression analysis) — статистический метод, используемый в эконометрике для оценки уравнения, которое в наибольшей мере соответствует совокупности наблюдений зависимых переменных и независимых переменных и тем самым дающий наилучшую оценку истинного соотношения между этими переменными. С помощью оцененного таким образом уравнения можно предсказать, какой будет (неизвестная) зависимая переменная для данного значения (известной) независимой переменной.

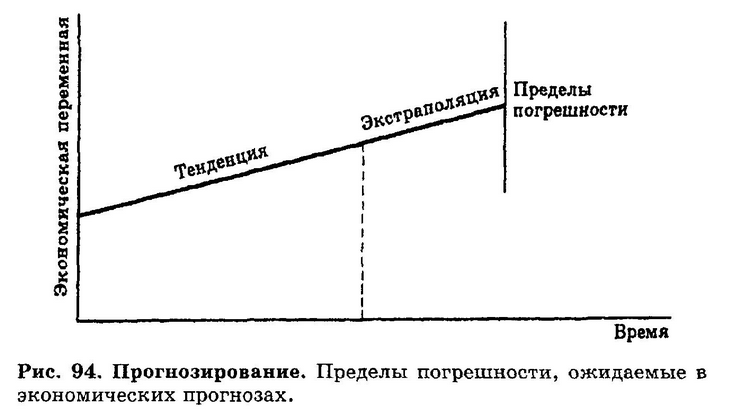
Если взять простейший пример линейного уравнения со всего одной независимой переменной и одной зависимой переменной (скажем, располагаемый доход и потребительские расходы), задача будет заключаться в подборе прямой линии к совокупности данных, состоящих из пар наблюдений дохода (Y) и потребления (С). На рис. 104 графически представлено множество таких пар наблюдаемых значений, и нам нужно найти уравнение прямой линии, которая лучше всего подходит к нашим данным, так как эта линия даст лучшие прогнозы зависимой переменной. Линию, которая лучше всего подходит к данным, нужно выбирать так, чтобы сумма квадратов значений вертикальных отклонений точек от линии была минимальной. Этот метод наименьших квадратов применяется при анализе большинства регрессий. Степень приближения регрессионной линии к наблюдениям измеряется коэффициентом корреляции.

Эти постоянные (а и b), полученные методом наименьших квадратов, называются оцененными коэффициентами регрессии. После того как их численные значения определены, они могут использоваться для предсказания значений зависимой переменной (С) на основе значений независимой переменной (Y). Например, если оцененные коэффициенты регрессии а и b равны 1000 и 0.9 соответственно, уравнение регрессии будет выглядеть как    С = 1000 + 0.9Y, и мы можем предсказать, что при располагаемом доходе         10 000 потребительские расходы составят

C = a + bY,

С = 1000 + 0.9Y =

= 1000+ 0.9 * 10000 =

= 10000.

Коэффициент наклона линии регрессии (b) особенно важен в экономической науке, так как он показывает изменение зависимой переменной (в данном случае потребления), вызываемое изменением независимой переменной (в данном случае дохода) на одну единицу. Например, значение b, равное 0.9, предполагает, что население тратит на потребление 90% дополнительного дохода.

Регрессионное уравнение не даёт точного прогноза зависимой переменной для любого заданного значения независимой переменной, так как коэффициенты регрессии, оцененные на основе выборочных наблюдений, являются лишь наилучшей оценкой действительных характеристик совокупности и подвержены случайным искажениям. Чтобы учесть погрешности оцененного уравнения регрессии, изображающего действительные закономерности поведения всего населения на основе выборочного наблюдения, уравнение регрессии обычно записывают как

                                                                                  С = a + bY + е,

где е — дополнительный остаточный член — отражает остаточное действие случайной вариации и действие других независимых переменных (например, влияние процентных ставок на потребительский кредит), которые воздействуют на потребительские расходы, но в уравнение регрессии явным образом не включены.

Там, где предполагается, что на зависимую переменную существенно влияет более чем одна независимая переменная, используется метод множественной линейной регрессии. Этот метод предполагает составление уравнения множественной линейной регрессии, включающей две или больше независимых переменных, как например

                                                                                С = а + bY + dI + е,

где I — ставка процента по потребительскому кредиту, a d является дополнительным коэффициентом регрессии, относящимся к этой дополнительной независимой переменной. Оценка этого уравнения множественной регрессии методом наименьших квадратов предполагает подбор трёхмерной плоскости к совокупности выборочных наблюдений потребительских расходов, располагаемого дохода и процентных ставок таким образом, чтобы минимизировать квадраты отклонений наблюдаемых значений от плоскости. Выборочные наблюдения могут использоваться для нахождения числовых оценок трёх коэффициентов регрессии (а, b и d) в указанном уравнении.

См. ПРОГНОЗИРОВАНИЕ.

ПРОГНОЗИРОВАНИЕ (forecasting) — процесс разработки предсказаний по поводу будущих общеэкономических и рыночных условий как основа для принятия решений государством и фирмами. Для оценки будущих экономических условий могут применяться различные прогностические методы, отличающиеся друг от друга по степени субъективности, сложности, потребности в данных и по стоимости:

(а) обследования — интервью или рассылка по почте анкет с целью выяснить будущие намерения в плане покупок потребителей и промышленных покупателей. Оценки будущих объёмов продаж могут давать также сотрудники отделов сбыта; кроме того, отраслевые эксперты могут разрабатывать сценарии будущего развития рынка;

(б) экспериментальные методы — прогнозирование спроса на новые продукты и т. д., базирующееся на анализе реакции либо небольших выборок потребителей, либо больших выборок на пробных рынках;

(в) методы экстраполяции - анализ временных рядов с использованием экономических данных за прошлые периоды для прогнозирования будущих тенденций. Эти методы неявно предполагают, что временные взаимосвязи, наблюдавшиеся в прошлом, будут сохраняться и в будущем, при этом не исследуются причинно-следственные связи между рассматриваемыми переменными. Временные ряды обычно включают в себя долгосрочную тенденцию (вековой тренд), нарушаемую среднесрочными циклическими колебаниями, и краткосрочные сезонные вариации, подвергающиеся нерегулярным, случайным воздействиям. Для анализа и экстраполяции таких временных рядов могут использоваться также такие методы, как скользящая средняя или экспоненциальное сглаживание, хотя с их помощью, как правило, нельзя предсказать резкие скачки экономических переменных;

(г) барометрические прогнозы — предсказание будущих значений экономических переменных исходя из текущих значений определённых статистических показателей, тесно связанных с экономическими переменными. Такие опережающие индикаторы, как планируемые капиталовложения предпринимательского сектора и прирост нового жилищного строительства, могут служить барометром при прогнозировании уровня экономической активности или спроса на продукцию, а кроме того, они могут быть пригодны для предсказания резких изменений этих величин;

(д) метод «затраты—выпуск» (см. модель «затраты —выпуск») — использование таблиц «затрат—выпуска» для отображения взаимосвязей между отраслями и для анализа того, как изменение спроса в одной отрасли влияет на изменение условий спроса и предложения в других, связанных с нею. Так, изготовителям узлов автомобиля необходимо оценивать спрос на автомобили и производственные планы автомобилестроителей, являющихся главными потребителями их продукции;

(е) эконометрические методы — прогнозирование будущих значений экономических переменных путём исследования других переменных, связанных причинно-следственными зависимостями с первыми. В эконометрических моделях переменные связаны между собою уравнениями, которые могут быть подвергнуты статистической проверке, а затем использованы как основа для прогнозирования. Необходимо прежде всего выявить независимые переменные, влияющие на зависимую переменную, величину которой мы прогнозируем.

Так, чтобы предсказать будущий объём спроса на продукт (Q_d), нам надлежит сформулировать уравнение, связывающее объём спроса с ценой продукта (Р) и располагаемым доходом (Y):

                                                                                        Q_d = а + bР + cY,

а затем использовать данные за прошлые периоды, чтобы определить коэффициенты регрессии а, b и с (см. РЕГРЕССИОННЫЙ АНАЛИЗ). Эконометрические модели могут состоять из одного уравнения (как в нашем случае), но зачастую в сложных экономических ситуациях независимые переменные одного уравнения сами подвержены влиянию других переменных, так что может потребоваться множество уравнений, чтобы отразить все причинно-следственные зависимости. Так, в модели макроэкономического прогнозирования, используемой британским министерством финансов для прогнозирования будущей экономической активности, содержится более 600 уравнений.

Ни один прогностический метод не даёт абсолютно точных предсказаний, поэтому, делая любой прогноз, необходимо учитывать пределы погрешности этого прогноза. В ситуации, показанной на рис. 94, невозможно точно определить будущее значение экономической переменной. Необходимо учесть, что существует область возможных будущих значений с центром в прогнозируемой точке, т. е. область значений с соответствующим распределением их вероятностей.

Контакты